

Next: Adhesive Borders
Up: Mathematical Models for the
Previous: Adhesion in an Assembly
We now turn attention to thin tubules, whose cross-section is simply modelled as a curve c,
whose length 2L is fixed. We aim at obtaining the equilibrium condition that holds at the
points like p* in Figure 7, where c detaches itself from a rigid wall, making no
assumptions on the symmetry of both c and the wall.
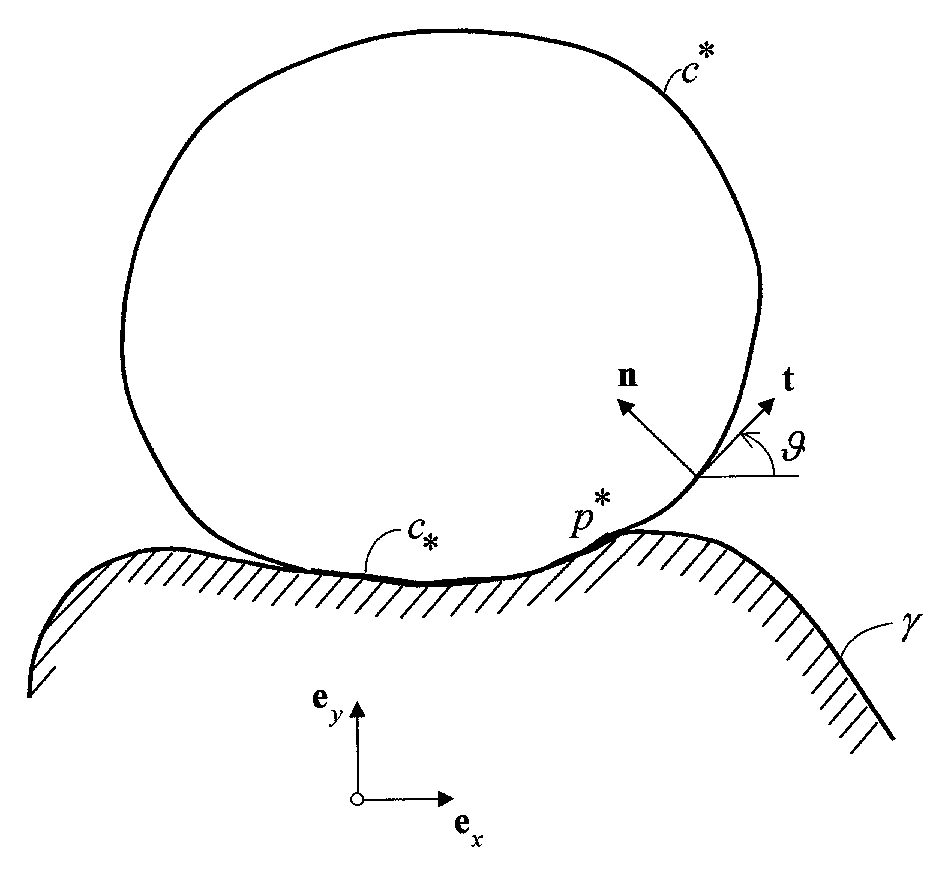
Figure 7. The contour of a lipid tubule adhering to a curved wall.
The elastic energy is modelled according to (1), with
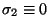 and
and
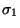 set equal to the curvature
set equal to the curvature 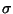 of c. The adhesion energy is modelled by
of c. The adhesion energy is modelled by
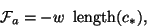 |
(11) |
where c* is the portion of c that adheres to the wall. It is shown in [12] that
the detachment equilibrium condition is the following:
![\begin{displaymath}[\hspace{-0.05cm}[\frac{{\mathrm d}\psi}{{\mathrm d}\sigma}]\...
...rac{{\mathrm d}\psi}{{\mathrm d}\sigma}]\hspace{-0.05cm}]-w=0,
\end{displaymath}](img49.png) |
(12) |
where
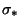 is the curvature of the wall at a detachment point p*. The
jump
is the curvature of the wall at a detachment point p*. The
jump
![$[\hspace{-0.05cm}[g ]\hspace{-0.05cm}]$](img51.png) of a function g is defined as
of a function g is defined as
![\begin{displaymath}[\hspace{-0.05cm}[g ]\hspace{-0.05cm}]:=\lim_{p \stackrel{p\i...
...ow}p^{*}}g-
\lim_{p \stackrel{p\in c^{*}}{\rightarrow}p^{*}}g,
\end{displaymath}](img52.png) |
(13) |
where c* is the free part of c. When 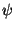 is taken to be a quadratic
function of
is taken to be a quadratic
function of 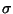 ,
that is,
,
that is,
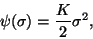 |
(14) |
equation (12) gives the following adhesion condition
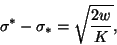 |
(15) |
where
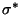 is the curvature of c* at p*. Equation (15)
generalizes the adhesion condition found by Seifert & Lipowsky in [6] for flat walls.
As an application, we have studied the adhesion of tubules to a groove modelled as a
hollow half-cylinder with radius R (see Figure 8).
is the curvature of c* at p*. Equation (15)
generalizes the adhesion condition found by Seifert & Lipowsky in [6] for flat walls.
As an application, we have studied the adhesion of tubules to a groove modelled as a
hollow half-cylinder with radius R (see Figure 8).
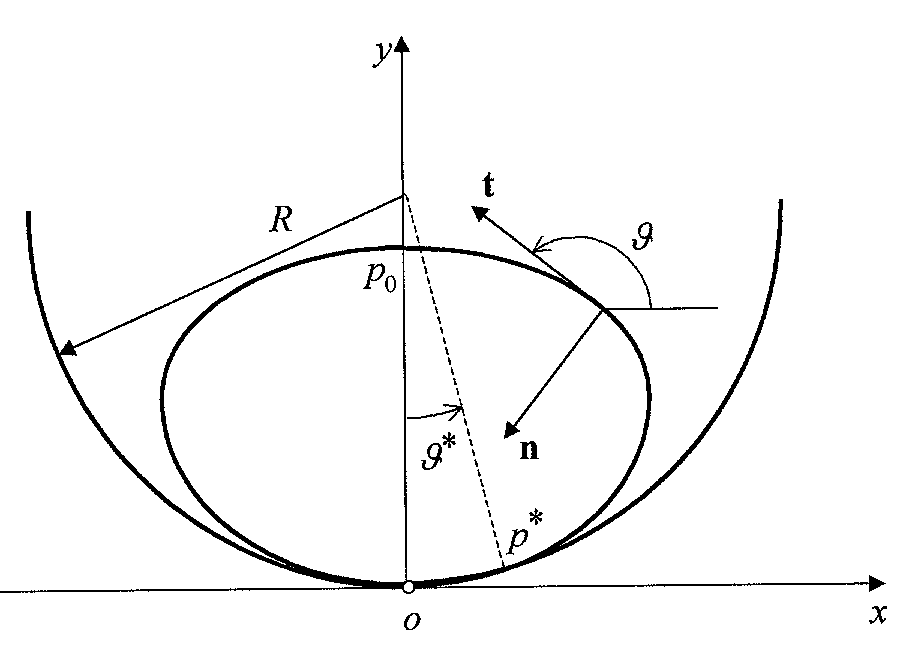
Figure 8. The contour of a tubule attached to a groove.
The existence of equilibrium solutions depends on the values of the dimensionless
parameters
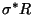 and
and
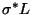 .
It turns out (see [12]) that there
exists precisely one equilibrium solution whenever
.
It turns out (see [12]) that there
exists precisely one equilibrium solution whenever
 is such that
is such that
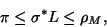 |
(16) |
where 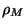 is a function of
is a function of
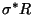 .
In [11], we studied by a similar
method the adhesion of a lipid tubule to a flat wall, and we only found a lower
bound L0 on L, above which there is precisely one equilibrium contour for an
adhering tubule:
.
In [11], we studied by a similar
method the adhesion of a lipid tubule to a flat wall, and we only found a lower
bound L0 on L, above which there is precisely one equilibrium contour for an
adhering tubule:
Since
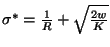 ,
it turns out that for a tubule adhering
to a groove the lower bound on L is smaller than L0. This is one way the curvature of
the wall acts: it promotes the adhesion of narrower tubules. Another way is again suggested
by (16): the upper bound on L prevents large tubules from adhering to a groove.
This is, however a less surprising result, as it essentially reflects a geometric obstruction.
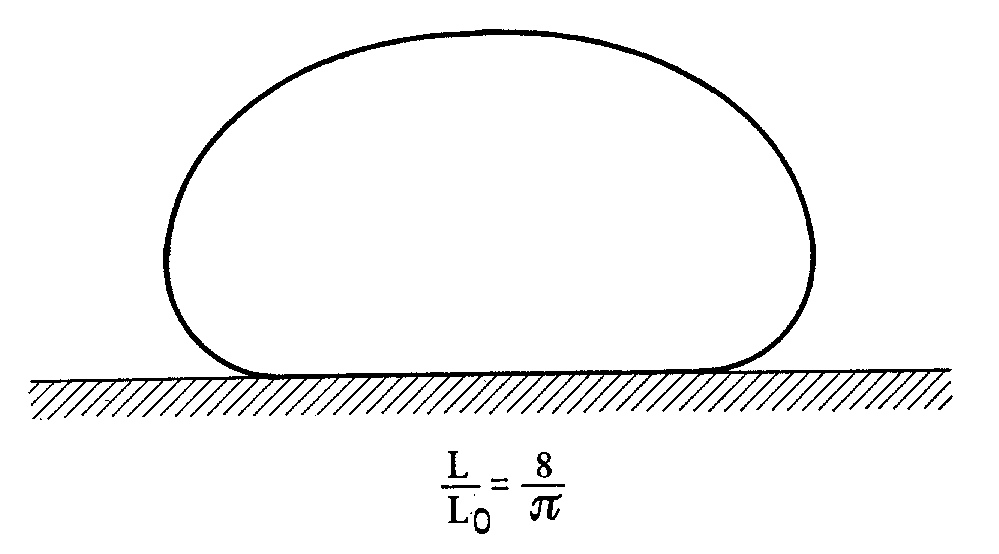
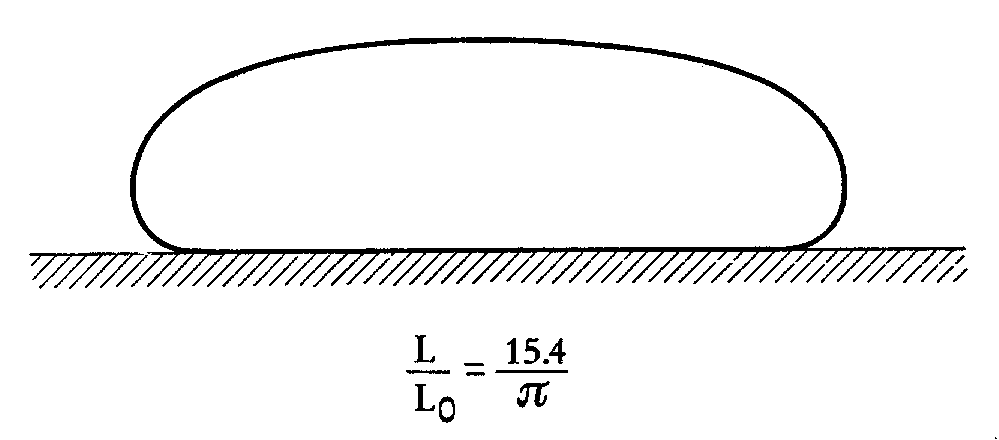
Figures 9a and 9b show, respectively, some equilibrium contours of tubules adhering either
to a flat wall or to a groove. These contours were obtained by means of the geometric
construction illustrated in the previous section, which relies upon the knowledge of the
curvature of the tubule's contour as a function of the angle
,
it turns out that for a tubule adhering
to a groove the lower bound on L is smaller than L0. This is one way the curvature of
the wall acts: it promotes the adhesion of narrower tubules. Another way is again suggested
by (16): the upper bound on L prevents large tubules from adhering to a groove.
This is, however a less surprising result, as it essentially reflects a geometric obstruction.
Figures 9a and 9b show, respectively, some equilibrium contours of tubules adhering either
to a flat wall or to a groove. These contours were obtained by means of the geometric
construction illustrated in the previous section, which relies upon the knowledge of the
curvature of the tubule's contour as a function of the angle 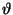 .
.
a)
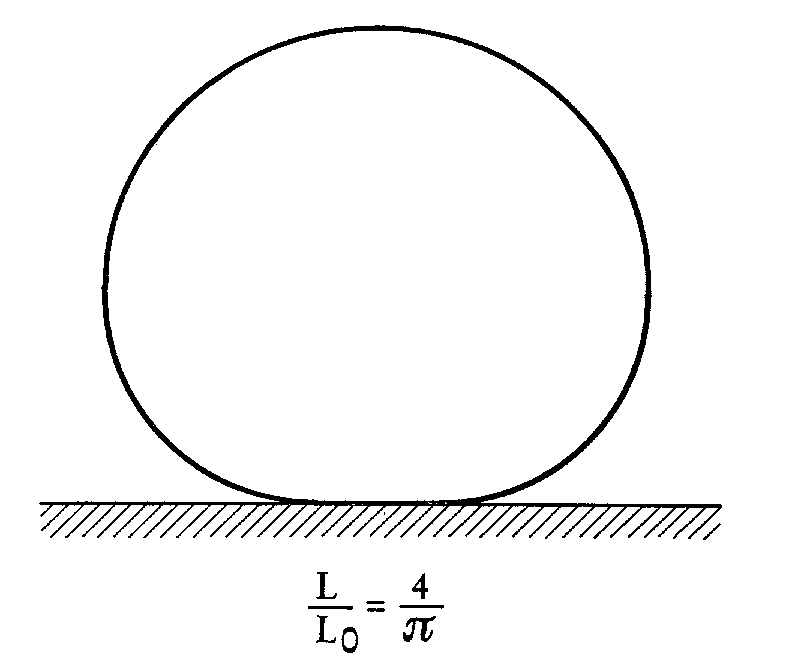
b)


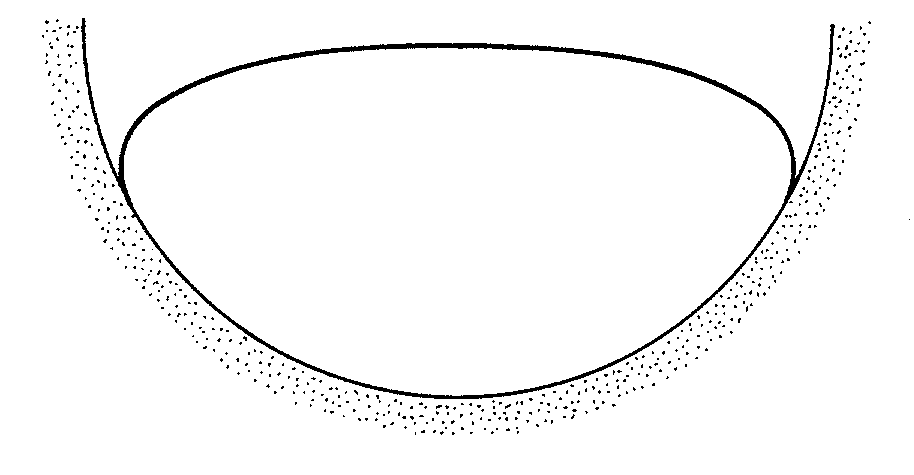
Figure 9. (a) Equilibrium contours of the same tubule for different values
of L0: from left to right,
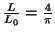 ,
,
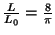 ,
and
,
and
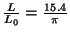 .
In this sequence the adhesion potential w increases,
and so does the length of the adhesion segment. (b) Equilibrium contours of a tubule adhering
to a groove, for different values of
.
In this sequence the adhesion potential w increases,
and so does the length of the adhesion segment. (b) Equilibrium contours of a tubule adhering
to a groove, for different values of
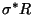 :
from left to right,
:
from left to right,
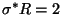 ,
,
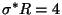 ,
and
,
and
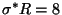 .
All these figures are drawn for
.
All these figures are drawn for
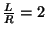 .
.


Next: Adhesive Borders
Up: Mathematical Models for the
Previous: Adhesion in an Assembly
Andre Sonnet
1999-06-28


![]() and
and
![]() set equal to the curvature
set equal to the curvature ![]() of c. The adhesion energy is modelled by
of c. The adhesion energy is modelled by

![]() and
and
![]() .
It turns out (see [12]) that there
exists precisely one equilibrium solution whenever
.
It turns out (see [12]) that there
exists precisely one equilibrium solution whenever
![]() is such that
is such that
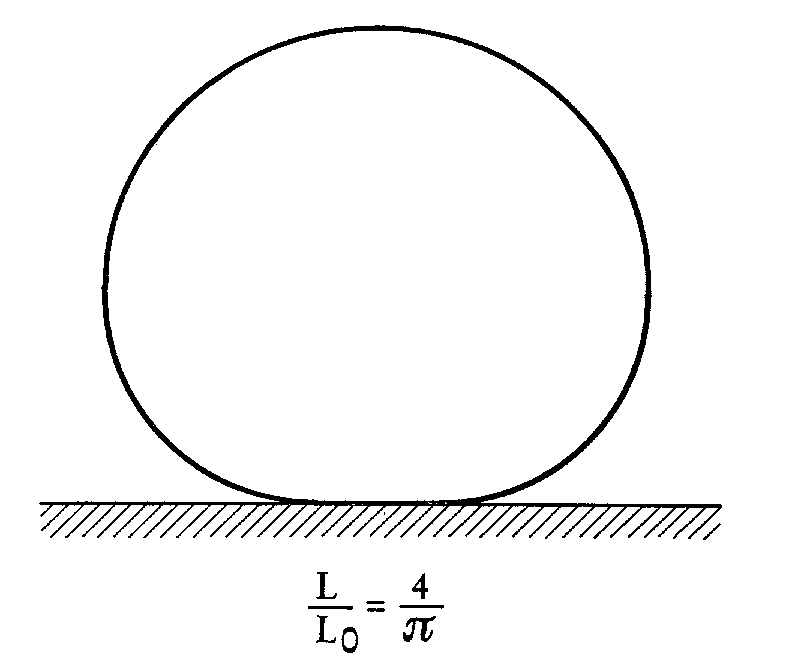





![]() ,
,
![]() ,
and
,
and
![]() .
In this sequence the adhesion potential w increases,
and so does the length of the adhesion segment. (b) Equilibrium contours of a tubule adhering
to a groove, for different values of
.
In this sequence the adhesion potential w increases,
and so does the length of the adhesion segment. (b) Equilibrium contours of a tubule adhering
to a groove, for different values of
![]() :
from left to right,
:
from left to right,
![]() ,
,
![]() ,
and
,
and
![]() .
All these figures are drawn for
.
All these figures are drawn for
![]() .
.